Analysis of Beams

Abstract

A beam is a structural element that is capable of withstanding load primarily by resisting bending. The bending force induced into the material of the beam as a result of the external loads, own weight, span and external reactions to these loads is called a bending moment.

Beams are traditionally descriptions of a building or civil engineering structural elements, but smaller structures such as a truck or automobile frames, machine frames, and other mechanical or structural systems contain beam structures that are designed and analyzed similarly.

This project deals with the computational calculation using MATLAB to get the shear force, bending moment diagrams, the deflected shape along with other analytical details of beams under different types of loadings. The entirely independent software was coded in MATLAB which could calculate all these aspects of a beam under any type and size of loading. This design-oriented-project was done under the supervision of Assistant Professor Dr. Dipendu Bhunia.

Types of Beams

• Simply supported: a beam supported on the ends which are free to rotate and have no moment resistance.
• Fixed: a beam supported on both ends and restrained from rotation.
• Over hanging: a simple beam extending beyond its support on one end.
• Continuous: a beam extending over more than two supports.
• Cantilever: a projecting beam fixed only at one end.
• Trussed: a beam strengthened by adding a cable or rod to form a truss.

Simply supported beam under different load

A beam supported by pins, rollers, or smooth surfaces at the ends is called a simple beam. A simple support will develop a reaction normal to the beam, but will not produce a moment at the reaction. If either, or both ends of a beam projects beyond the supports, it is called a simple beam with overhang.

It is possible to observe that longitudinal elements of the beam near the bottom are stretched and those near the top are compressed, thus indicating the simultaneous existence of both tensile and compressive stresses on transverse planes. These stresses are designated fiber or flexural stresses. A free body diagram of the portion of the beam between the left end and plane a-a. A study of this section diagram reveals that a transverse force Vr and a couple Mr at the cut section and a force, R, (a reaction) at the left support are needed to maintain equilibrium. The force Vr is the resultant of the shearing stresses at the section (on plane a-a) and is called the resisting shear and the moment, Mr, is the resultant of the normal stresses in the section and is called the resisting moment.

Under point load

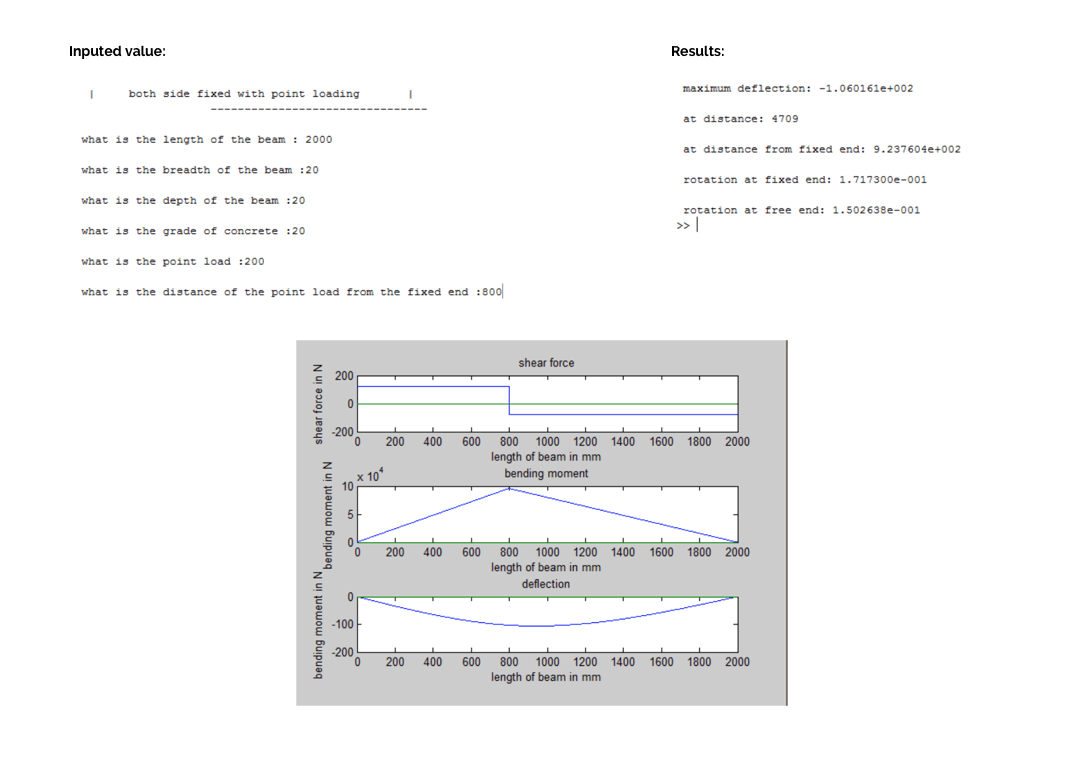
Sample output for the above code under point loadings

Under uniform load

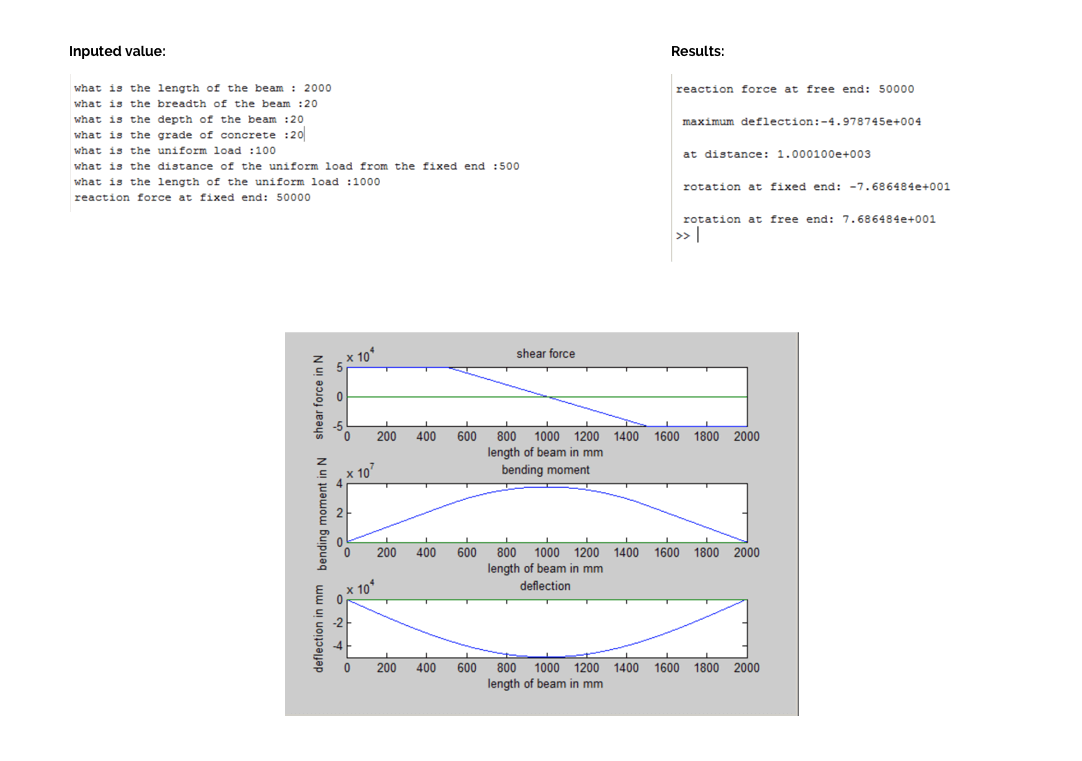
Sample output for the above code under uniform loadings

User interface

I also created an easy to use user interface for users to feed in the details of the beam and to show the output in a clear and simple manner. This required knowledge of creating interfaces using a computation tool like MATLAB.

Here are the glimpses of the GUI-

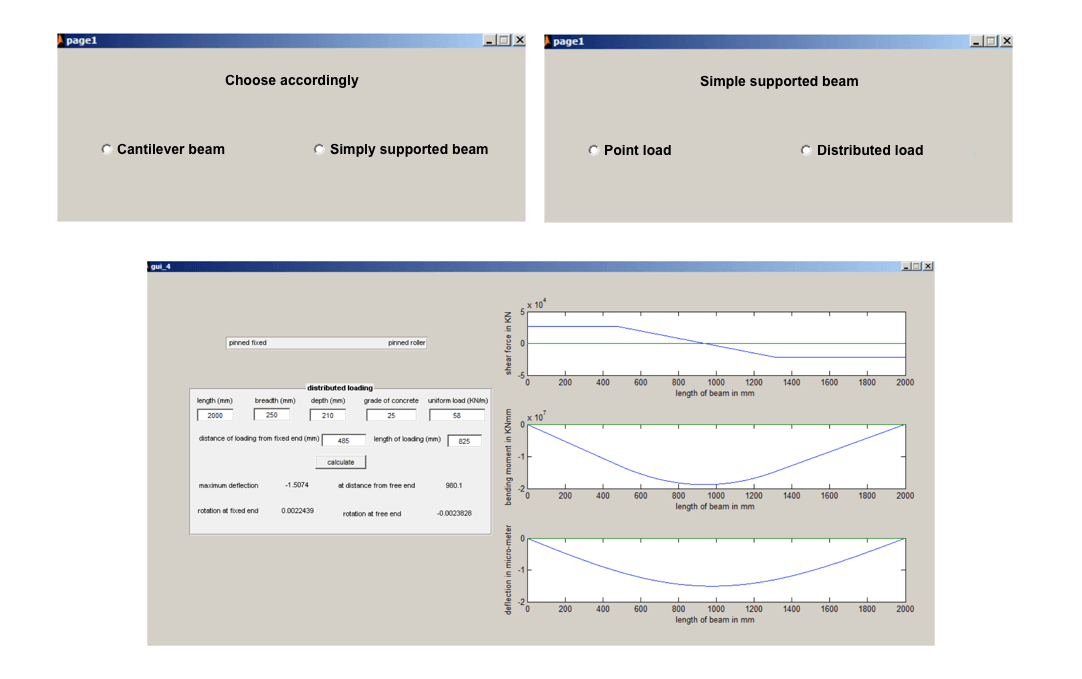
Similarly, one can make calculations for other beams with various dimensions within seconds

Outcome

This project required me to supplement my theoretical knowledge of structures with computational skills and mathematical tools. I was able to successfully provide an analysis of cantilever, simply supported and other types of beams under any loadings. This software, at the time of being built, was amongst the only few tools which could provide this information of beams with such ease. This project helped me understand the importance of learning interdisciplinary subjects and combining them in creative ways.